

A Treatise on the Theory of Determinants. "A Spectral Characterization of Hermitian Centrosymmetric and Hermitian Skew-Centrosymmetric K-Matrices". If we multiply a symmetric matrix by a scalar, the result will be a symmetric matrix. "Characterization and properties of matrices with generalized symmetry or skew symmetry". The sum of two symmetric matrices is a symmetric matrix. "A spectral characterization of generalized real symmetric centrosymmetric and generalized real symmetric skew-centrosymmetric matrices". In this section, we will revisit the theory of eigenvalues and eigenvectors for the special class of matrices that are symmetric, meaning that the matrix. "Some properties of commuting and anti-commuting m-involutions". The characteristics of symmetric matrices are as follows: The addition (or subtraction) of two symmetric matrices results in another symmetric matrix. A similar result holds for Hermitian centrosymmetric and skew-centrosymmetric matrices. Then A is diagonalizable with real eigenvalues 1, , N (repeated. This statement is not true, in general, for a symmetric. When the ground field is the field of real numbers, it has been shown that bisymmetric matrices are precisely those symmetric matrices whose eigenvalues remain the same aside from possible sign changes following pre- or post-multiplication by the exchange matrix. It is well known that a real symmetric matrix can be diagonalised by an orthogonal transformation. Symmetric centrosymmetric matrices are sometimes called bisymmetric matrices. The inverse problem for the commutation relation AK = KA of identifying all involutory K that commute with a fixed matrix A has also been studied. The centrosymmetric relation AJ = JA lends itself to a natural generalization, where J is replaced with an involutory matrix K (i.e., K 2 = I) or, more generally, a matrix K satisfying K m = I for an integer m > 1. Equivalently, A is skew-centrosymmetric if AJ = − JA, where J is the exchange matrix defined above. Step 3: If the transpose of the matrix is equal to the matrix itself, then it is a symmetric matrix.Question 4: Explain a skew symmetric matrix Answer: A matrix can be skew.
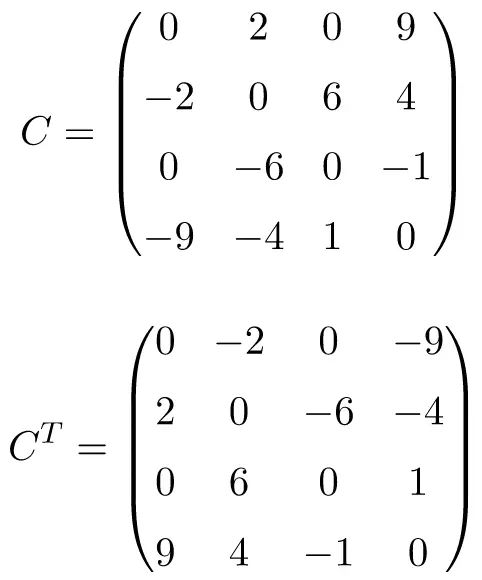
Step 2: Find the transpose of the given matrix. Answer: Symmetric matrix refers to a matrix in which the transpose is equal to itself.A symmetric matrix A therefore satisfies the condition, A A T.

The transpose matrix of any given matrix A can be given as A T. Step 1: First, check if it's a square matrix, as only square matrices can be considered as symmetric matrices. We could either use a different C++ type or use Eigens triangular views. In linear algebra, a symmetric matrix is defined as the square matrix that is equal to its transpose matrix.Here, is the coefficient of in for, is the coefficient of the term in is that of and is the constant term. for an appropriate symmetric matrix, vector and scalar. Therefore, it has all the properties that a symmetric matrix has. Indeed, any quadratic function can be written as. The symmetric matrices are simply the Hermitian matrices but with the conjugate transpose being the same as themselves. These are the steps to find symmetric matrix: There is a natural relationship between symmetric matrices and quadratic functions. How Do You Find if a Matrix is a Symmetric Matrix? This can be represented as: If B = \(\left[\mathrm\). Comment: To triangulate the matrix, use induction of the order of the matrix. Of course, symmetric matrices are much more special than just being normal, and indeed the argument above does not prove the stronger result that symmetric matrices are orthogonaly diagonalizable. Consider the given matrix B, that is, a square matrix that is equal to the transposed form of that matrix, called a symmetric matrix. Of course, the result shows that every normal matrix is diagonalizable. Symmetric Matrix DefinitionĪ square matrix B which of size n × n is considered to be symmetric if and only if B T = B.

That means, a matrix whose transpose is equal to the matrix itself, is called a symmetric matrix. A symmetric matrix in linear algebra is a square matrix that remains unaltered when its transpose is calculated.


 0 kommentar(er)
0 kommentar(er)
